Possible Straight Hands In Poker
- Poker starting hand combinations basics. AK or T5) = 16 combinations; Pairs (e.g. AA or TT) = 6 combinations; If you were take a hand like AK and write down all the possible ways you could be dealt this hand from a deck of cards (e.g. A K, A K, A K etc.), you would find that there are 16 possible combinations. See all 16 AK hand.
- Eliminating identical hands that ignore relative suit values leaves 6,009,159 distinct 7-card hands. The number of distinct 5-card poker hands that are possible from 7 cards is 4,824. Perhaps surprisingly, this is fewer than the number of 5-card poker hands from 5 cards because some 5-card hands are impossible with 7 cards (e.g.
- POKER PROBABILITIES (FIVE CARD HANDS) In many forms of poker, one is dealt 5 cards from a standard deck of 52 cards. The number of different 5 -card poker hands is. 52 C 5 = 2,598,960. A wonderful exercise involves having students verify probabilities that appear in books relating to gambling.
With a huge games selection, 24/7 support & regular bonuses, Videoslots well deserves their popularity. Make a deposit How Many Possible Poker Hands Are A Straight Flush to receive a 100% bonus up to £200 + 11 welcome spins.
Sanderson M. Smith
Home About Sanderson Smith Writings and Reflections Algebra 2 AP Statistics Statistics/Finance Forum
In many forms of poker, one is dealt 5 cards from astandard deck of 52 cards. The number of different 5 -card pokerhands is
A wonderful exercise involves having students verify probabilitiesthat appear in books relating to gambling. For instance, inProbabilities in Everyday Life, by John D. McGervey, one findsmany interesting tables containing probabilities for poker and othergames of chance.
This article and the tables below assume the reader is familiarwith the names for various poker hands. In the NUMBER OF WAYS columnof TABLE 2 are the numbers as they appear on page 132 in McGervey'sbook. I have done computations to verify McGervey's figures. Thiscould be an excellent exercise for students who are studyingprobability.
There are 13 denominations (A,K,Q,J,10,9,8,7,6,5,4,3,2) in thedeck. One can think of J as 11, Q as 12, and K as 13. Since an acecan be 'high' or 'low', it can be thought of as 14 or 1. With this inmind, there are 10 five-card sequences of consecutive dominations.These are displayed in TABLE 1.
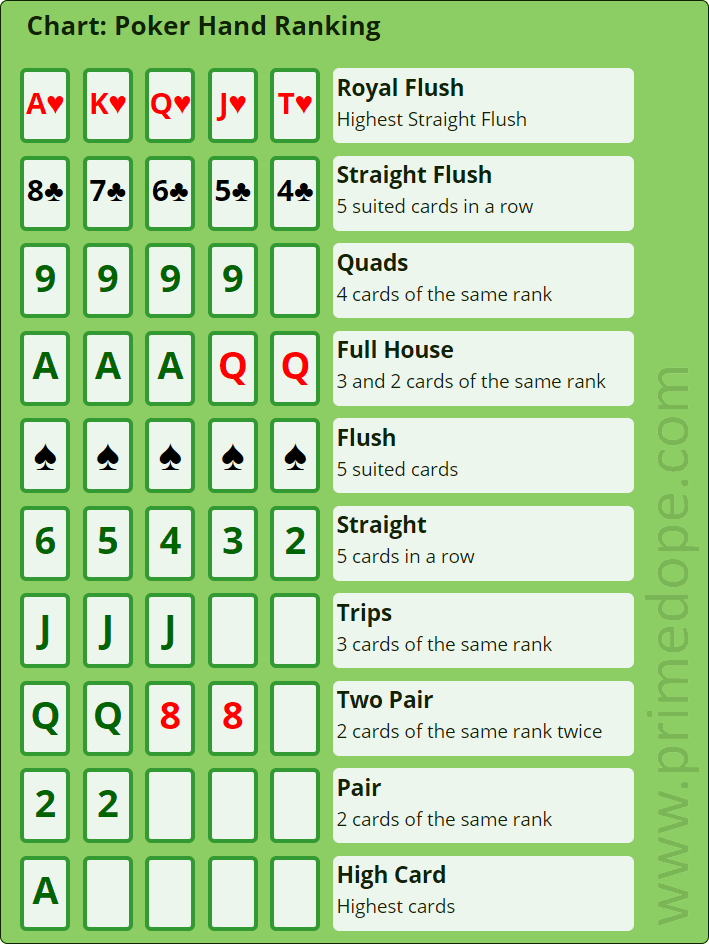TABLE 1The following table displays computations to verify McGervey'snumbers. There are, of course , many other possible poker handcombinations. Those in the table are specifically listed inMcGervey's book. The computations I have indicated in the table doyield values that are in agreement with those that appear in thebook.
N = NUMBER OF WAYS listed by McGervey | |||
Straight flush | There are four suits (spades, hearts, diamond, clubs). Using TABLE 1,4(10) = 40. | ||
Four of a kind | (13C1)(48C1) = 624. Choose 1 of 13 denominations to get four cards and combine with 1 card from the remaining 48. | ||
Full house | (13C1)(4C3)(12C1)(4C2) = 3,744. Choose 1 denominaiton, pick 3 of 4 from it, choose a second denomination, pick 2 of 4 from it. | ||
Flush | (4C1)(13C5) = 5,148. Choose 1 suit, then choose 5 of the 13 cards in the suit. This figure includes all flushes. McGervey's figure does not include straight flushes (listed above). Note that 5,148 - 40 = 5,108. | ||
Straight | (4C1)5(10) = 45(10) = 10,240 Using TABLE 1, there are 10 possible sequences. Each denomination card can be 1 of 4 in the denomination. This figure includes all straights. McGervey's figure does not include straight flushes (listed above). Note that 10,240 - 40 = 10,200. | ||
Three of a kind | (13C1)(4C3)(48C2) = 58,656. Choose 1 of 13 denominations, pick 3 of the four cards from it, then combine with 2 of the remaining 48 cards. This figure includes all full houses. McGervey's figure does not include full houses (listed above). Note that 54,912 - 3,744 = 54,912. | ||
Exactly one pair, with the pair being aces. | (4C2)(48C1)(44C1)(40C1)/3! = 84,480. Choose 2 of the four aces, pick 1 card from remaining 48 (and remove from consider other cards in that denomination), choose 1 card from remaining 44 (and remove other cards from that denomination), then chose 1 card from the remaining 40. The division by 3! = 6 is necessary to remove duplication in the choice of the last 3 cards. For instance, the process would allow for KQJ, but also KJQ, QKJ, QJK, JQK, and JKQ. These are the same sets of three cards, just chosen in a different order. | ||
Two pairs, with the pairs being 3's and 2's. | McGervey's figure excludes a full house with 3's and 2's. (4C2)(4C1)(44C1) = 1,584. Choose 2 of the 4 threes, 2 of the 4 twos, and one card from the 44 cards that are not 2's or 3's. |
'I must complain the cards are ill shuffled 'til Ihave a good hand.'
-Swift, Thoughts on Various Subjects
Home About Sanderson Smith Writings and Reflections Algebra 2 AP Statistics Statistics/Finance Forum
Previous Page Print This Page
Copyright © 2003-2009 Sanderson Smith
Every poker player knows that the Royal Flush is the strongest poker hand, but where do all of the other poker winning hands rank? Here is a comprehensive list of poker hands in order from highest to lowest ranking. If you are new to the game of poker, learning the different poker hands is a great first step in learning how to beat your opponents with the cards you are dealt.
#1 Royal Flush
The strongest poker hand is the royal flush. It consists of Ten, Jack, Queen, King, and Ace, all of the same suit, e.g. diamonds, spades, hearts, or clubs.
#2 Straight Flush
The second strongest hand in poker is the straight flush. It is composed of five consecutive cards of the same suit. If two players have a straight flush, the player with the highest cards wins.
#3 Four-of-a-kind
A four-of-a-kind is four cards of the same rank, e.g. four Aces. If two players have four-of-a-kind, then the one with the highest four-of-a-kind wins. If they have the same (if four-of-a-kind is on the board), then the player with the highest fifth card wins, since a poker hand is always composed of five cards.
#4 Full House
A full house is a combination of a three-of-a-kind and a pair. If two players have a full house, then the one with the highest three-of-a-kind wins. If they have the same one, then the pair counts.
#5 Flush
Five cards of the same suit make a flush. If two players have a flush, then the one with the highest cards wins.
#6 Straight
Five consecutive cards are called a straight. If two players have a straight, the one with the highest cards wins.
#7 Three-of-a-kind
How To Get A Straight In Poker
A three-of-a-kind is composed of three cards of the same rank. If two players have the same three-of-a-kind, then the other cards, or both cards, determine the winner, since a poker hand is a always composed of five cards.
#8 Two-pair
Two-pair hands are, of course, composed of two pairs. If two players have two-pair, the rank of the higher pair determines the winner. If they have the same higher pair, then the lower one counts. If that is also the same, then the fifth card counts.
#9 Pair
A pair is composed of two cards of the same rank. Since a poker hand is always composed of five cards, the other three cards are so-called “kickers”. In case two players have the same pair, then the one with the highest kicker wins.
#10 High card
If you don’t even have a pair, then you look at the strength of your cards. If there are two players at showdown who don’t have a pair or better, then the one with the highest cards wins.
Any of the PalaPoker.com games use the standard rank of hands to determine the high hand.
However, at PalaPoker.com we also play “split pot” games, like Omaha Hi-Lo8 and Stud Hi-Lo8, in which the highest hand splits the pot with a qualifying (“8 or better”) low hand; therefore, we must also be familiar with:
Low Poker Hands List:
This method of ranking low hands is used in traditional Hi/Lo games, like Omaha Hi/Lo and Stud Hi/Lo, as well as in Razz, the ‘low only’ Stud game.
Note that suits are irrelevant for Ace to Five low. A flush or straight does not ‘break’ an Ace to Five low poker hand. Aces are always a ‘low’ card when considering a low hand.
Please also note that the value of a five-card low hand starts with the top card, and goes down from there.
#1 Five Low, or “Wheel“: The Five, Four, Three, Deuce and Ace.
In the event of a tie: All Five-high hands split the pot.
#2 Six Low: Any five unpaired cards with the highest card being a Six.
In the event of a tie: The lower second-highest ranking card wins the pot. Thus 6,4,3,2,A defeats 6,5,4,2,A. If necessary, the third-highest, fourth-highest and fifth-highest cards in the hand can be used to break the tie.
#3 Seven Low: Any five unpaired cards with the highest card being a Seven.
In the event of a tie: The lower second-highest ranking card wins the pot. If necessary, the third- highest, fourth-highest and fifth-highest cards in the hand can be used to break the tie.
Possible Straight Hands In Poker Games
#4 Eight Low: Any five unpaired cards with the highest card being an Eight.
In the event of a tie: The lower second-highest ranking card wins the pot. If necessary, the third-highest, fourth-highest and fifth-highest cards in the hand can be used to break the tie. An Eight Low is the weakest hand that qualifies for low in Omaha Hi/Lo and Stud Hi/Lo.
Possible Straight Hands In Poker
Check back here as you are learning the game of poker for a list that details the poker hands order. Sign up today to start winning real money!